Problemas de suma de fracciones y ejercicios resueltos

La forma más eficaz de aprender a dominar la suma y resta con fracciones es mediante la práctica. Es por eso que hoy queremos compartir contigo un formulario de problemas de suma de fracciones y ejercicios resueltos. Con la práctica podrás dominar este tipo de operaciones matemáticas. No te preocupes, te explicamos paso a paso.

Las fracciones fueron una de las operaciones matemáticas más importantes ideadas por el ser humano para resolver problemas de la vida cotidiana. A pesar de que hoy en día muchas personas ven las aplicaciones matemáticas como algo abstracto, lo cierto es que las fracciones tienen muchísima incidencia sobre casi cualquier cosa a nuestro alrededor.

Por eso, y por el hecho de ser un recurso indispensable para desenvolverse en la aritmética y otros campos de las matemáticas, es necesario dominar la suma, resta, multiplicación y división con fracciones. Continúa con nuestro formulario y empieza a practicar.

Representación de fracciones y problemas resueltos

Para resolver problemas de suma de fracciones es necesario saber cómo representar las fracciones en una expresión matemática, ya que con esto se hace mucho más simple empezar a realizar la suma de las distintas fracciones sin problema.

Dicho esto, la manera de saber cómo representar las “partes de un todo” por medio de una fracción consiste en identificar el numerador y el denominador. Veamos gráficamente un ejemplo.

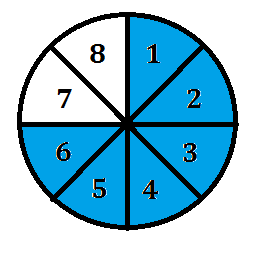
Fracción

En este caso, la figura mostrada está dividida en 8 partes, lo cual significa que el denominador de la fracción será 8. El denominador se coloca en la parte inferior de la fracción y representa el número total de partes que representa un “todo”, o también, el número de veces entre las cuales se divide el numerador.

De la misma manera, podemos observar que de las 8 partes, solo quedan 6, ya que las otras 2 han sido retiradas. Viendo esto, podemos darnos cuenta que el numerador, número de partes que aún quedan del “todo”. También puede definirse como el número de enteros que puede dividirse entre el denominador. Sabiendo esto, podríamos representar esta fracción cómo:

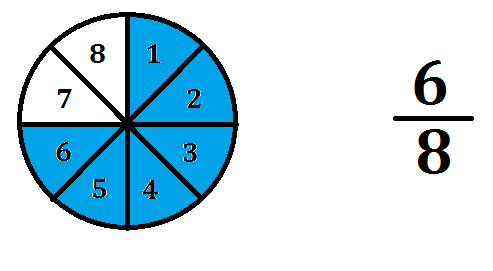
$Representación de una fracción$

Ahora bien, en problemas de la vida cotidiana, basta con identificar estos factores para poder representar matemáticamente una suma de fracciones. Veamos ejemplos prácticos:

Problema 1

Dos amigos salen a comer y piden una Pizza mediana de 8 trozos. El primero de ellos se come 3 trozos y el segundo se come 4 trozos. ¿Qué cantidad de pizza se comieron entre ambos? Represéntalo mediante una suma de fracciones.

Para resolver este problema vamos a representar la suma de la siguiente manera:

$\frac{3}{8}+\frac{4}{8}=?$

Recuerda que el denominador es el número total de partes que representa un “todo”, por lo que será el mismo para ambos casos. Del mismo modo, los numeradores (3) y (4) son las partes que han comido cada uno de los amigos. Realizamos esta suma de fracciones con igual denominador. Sumamos los numeradores y mantenemos el denominador común.

$\frac{3}{8}+\frac{4}{8}=\frac{4}{8}$

Respuesta: Entre ambos amigos se han comido 7/8 partes de la pizza, es decir, solo ha quedado un trozo de pizza.

En este problema nos hemos encontrado con una suma de fracciones con un denominador igual. Recuerda que existen otro tipo de suma de fracciones para los casos en los que nos encontramos con denominadores distintos. Para aprender con mayor detalle a resolver suma de fracciones con distinto denominador, visita este artículo.

Problema 2

En la antigua Persia, un comerciante de sal logra vender en la mañana medio kilo de sal. Durante la tarde consigue vender un kilo y medio de la misma. Finalmente en la noche antes de irse a dormir, un cliente le compra tres cuartas partes de un kilo de sal. ¿Cuánta sal ha vendido el comerciante persa al final de ese día?

Para resolver este problema debemos identificar nuevamente los numeradores y denominadores de cada fracción. Considerando que se han dividido las ventas de este hombre en tres fracciones, vamos a identificar cada una.

Medio kilo = ½
Kilo y medio = 1½
Tres cuartas partes de kilo= ¾

Ahora planteamos la operación:

$\frac{1}{2}+1\frac{1}{2}+\frac{3}{4}=?$

A continuación, hay que considerar que se trata de una suma de fracciones con distinto denominador (si no sabes cómo resolverlas, visita el artículo que te hemos recomendado). Resolvemos el ejercicio entonces:

$\frac{1}{2}+1\frac{1}{2}+\frac{3}{4}=\frac{8}{16}+1\frac{8}{16}+\frac{12}{16}= 2\frac{3}{4}$

De esta manera obtenemos que el comerciante ha logrado vender 2 ¾ kilos de sal (2 kilos y 750 gramos de sal).

Problema 3

Un inversionista logra ganar el equivalente a 50/10 partes de su inversión inicial en el primer año. Durante el segundo año pierde 30/10 parte de la misma. Sin embargo, para el tercer año las fluctuaciones de mercado le favorecen y vuelve a ganar 200/10 partes de su inversión inicial. Al final de año, ¿Cuántas partes de la inversión inicial ha logrado captar?

Al igual que como ocurre con casi todas las operaciones matemáticas, existe la resta de fracciones, una manera de reflejar por medio de “partes” la pérdida. En este caso, debemos aplicar la suma y resta de fracciones para dar con la respuesta. Planteamos el problema:

$\frac{50}{10}-\frac{30}{10}+\frac{200}{10}=\frac{220}{10}$

En este caso hemos aplicado la suma y resta de fracciones considerando que se trata de una operación de fracciones homogéneas (igual denominador).

El inversionista ha logrado ganar 220/10 partes de su inversión inicial. Es decir, ha multiplicado 22 veces el dinero que invirtió inicialmente en su proyecto.

Ejemplos resueltos de suma de fracciones

Si quieres practicar tú mismo en casa algunos ejemplos de suma de fracciones, puedes empezar por utilizar como guía de ejercicios los siguientes ejemplos resueltos de suma de fracciones:

$\frac{1}{4}+\frac{1}{3}=\frac{3}{12}+\frac{4}{12}=\frac{7}{12}$
$\frac{1}{2}+\frac{3}{4}+\frac{5}{3}=\frac{6}{12}+\frac{9}{12}+\frac{20}{12}=\frac{35}{12}$
$6\frac{3}{8}+4\frac{1}{2}=10\frac{14}{16}=10\frac{7}{8}$
$4\frac{1}{3}+2\frac{1}{2}=5\frac{5}{6}$
$\frac{2}{10}+\frac{5}{2}+\frac{8}{3}=\frac{12}{60}+\frac{150}{60}+\frac{160}{60}=\frac{370}{60}$
$\frac{2}{3}+\frac{4}{5}=\frac{10}{15}+\frac{12}{15}=\frac{22}{15}$
$\frac{1}{3}+\frac{2}{4}=\frac{4}{12}+\frac{6}{12}=\frac{10}{12}$

Ejercicios y problemas propuestos de suma de fracciones

Si ya has visto los ejemplos que recién hemos dejado para ti, puedes dar el siguiente paso y resolver tú mismo algunos ejercicios propuestos de suma de fracciones. De esta manera podrás adaptarte a diferentes tipos de planteamientos.

Una persona logra subir 15 pisos por las escaleras de un edificio en 10 minutos. Los 10 minutos siguientes asciende un total de 13 pisos más. Los últimos 10 minutos le sirven para subir 12 pisos más. Considerando que está ascendiendo por un edificio de 70 pisos de altura, ¿Cuántos pisos ha subido esta persona luego de pasada media hora? Aplica la suma de fracciones.
Un vendedor de helados vende 1/8 partes de toda su mercancía durante la mañana. Esa misma tarde consigue vender 1/3 de la mercancía. Finalmente durante el atardecer logra vender 2/5 partes de la mercancía. ¿Cuánto helado de toda la despensa ha vendido esta persona al terminar el atardecer?
Un equipo de constructores, durante de un día de trabajo soleado logra construir 3/20 parte de una pequeña obra. El segundo día, debido a condiciones climáticas, solo pueden avanzar 2/20 parte más de la construcción. Para el tercer día el clima mejora y logran progresar un 7/20. ¿Cuál es el progreso total que han logrado en los tres primeros días?