Ya hemos hablado numerosas veces de cómo las fracciones han ayudado al hombre. Desde las primeras civilizaciones, el uso de las matemáticas ha permitido al ser humano edificar muchos de sus sueños. En este sentido, las fracciones surgieron como una manera de plasmar numéricamente algunas situaciones de la matemática que hasta entonces no era posible. Tal es el caso de la suma de fracciones impropias y propias.
Antes de saber cómo realizar suma, resta y otras operaciones con fracciones, es indispensable conocer un poco más sobre ellas, así como también resulta importante saber qué son fracciones propias e impropias. Continúa leyendo para aprender todo lo necesario sobre este tema.
Las fracciones propias e impropias
Las fracciones han sido categorizadas por los matemáticos en tres grupos principales, cada uno de ellos tiene sus propias características y resulta importante identificarlas, ya que en función de ello podremos hacer cualquier tipo de operaciones como la suma de fracciones impropias y propias. Aprendamos un poco de cada una:
Fracciones propias
Las fracciones propias son aquellas representadas por un número cuyo valor es menor a 1, pero al mismo tiempo es mayor a 0. Una manera sencilla de reconocer una fracción propia, es considerando que éstas siempre poseen el denominador mayor al numerador.
Gráficamente podemos representar una fracción propia mediante este tipo de ejemplos:
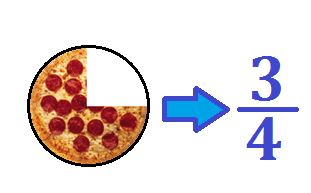
En este caso, la fracción mostrada (3/4) cuenta con un denominador de mayor valor que el numerador, por lo que podemos identificarla como una fracción propia. Además, el valor real de (3/4) es 0.75, un número mayor a 0 y menor que 1.
![]()
Fracciones impropias
Al contrario de lo que ocurre con las fracciones propias, una fracción impropia es aquella cuyo valor real es siempre mayor a 1. En estos casos, el denominador puede ser igual o menor al numerador. Volvemos a representarlo mediante una ilustración:
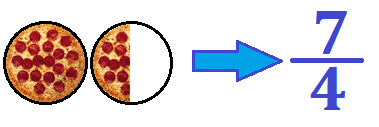
Este ejemplo refleja exactamente lo que es una fracción impropia. Se puede observar cómo el denominador es menor al numerador. Además, la fracción (7/4) tiene un valor numérico de 1.75, lo cual es mayor a 1 y representa una fracción impropia.
![]()
Fracciones mixtas
Las fracciones mixtas ya las hemos visto previamente en blogdematematicas, puedes ver el artículo de suma de fracciones mixtas. Una fracción mixta es aquella compuesta por un número entero y una fracción propia. Es decir, su valor real es mayor a 1 y puede representarse mediante un número entero acompañado de una fracción propia.
Las fracciones mixtas son otra de las formas en las cuales se puede representar una fracción impropia. Esto podemos ver utilizando el ejemplo anterior:
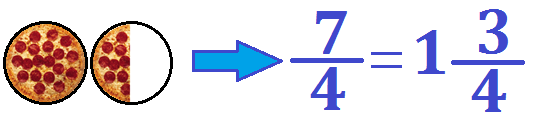
Consideramos en este caso que la fracción (7/4) puede ser expresada como (1¾).
![]()
Operaciones de suma con los distintos tipos de fracciones
Para realizar suma de fracciones impropias y propias basta con conocer las propiedades básicas de la suma de fracciones. Es decir, es suficiente con saber realizar suma de fracciones con igual y distinto denominador, ya que en esencia, no cambia el tipo de operación sin importar si se trata de fracciones propias o impropias.
Veamos algunos ejemplos de suma de fracciones donde se utilizan fracciones propias, impropias y mixtas.
Suma de fracciones impropias y propias con igual denominador
Este tipo de suma de fracciones es el más sencillo de realizar. Sin importar si se trata de fracciones propias o impropias, cuando el denominador de cada una de las fracciones que se encuentra en la operación es igual, el procedimiento que se aplica es el siguiente:
- Se deben sumar los numeradores de cada una de las fracciones.
- Es necesario conservar el mismo denominador común.
- Se escribe el producto de la suma colocando en el numerador el resultado de la suma de todos los denominadores. En el denominador se escribe el mismo denominador común.
- Veamos un ejemplo:
![]()
En este ejemplo hemos aplicado el procedimiento que recién explicamos. Adicionalmente, podemos observar que la primera fracción de la operación (7/4) es una fracción impropia, mientras que la segunda fracción (3/4) es una fracción propia.
Suma de fracciones impropias y propias con distinto denominador
En el caso de contar con fracciones con distinto denominador, independientemente si se trata de fracciones propias o impropias, es necesario aplicar un paso extra con respecto al caso anterior. Esto se debe a que es necesario homogeneizar los denominadores de la operación. Lo que debemos hacer se muestra a continuación:
- Aplicar el método de m.c.m o método de la cruz para obtener un denominador común de todos los denominadores distintos que se encuentran en la suma de fracciones.
- Si utilizamos el método de la cruz, el denominador común de la suma de fracciones será obtenida como el producto de la multiplicación de todos los denominadores involucrados en la suma.
- Si utilizamos el método de la cruz, para obtener el (los) nuevo(s) numerador(es) se debe multiplicar el numerador de cada fracción por el (los) denominador (res) de las otras fracciones involucradas.
- Se deben sumar los nuevos numeradores de cada una de las fracciones.
- Debes conserva el mismo denominador común.
- Escribe el producto de la suma colocando en el numerador el resultado de la suma de todos los denominadores. En el denominador se escribe el mismo denominador común.
- Veamos un ejemplo:
![]()
Este ejemplo refleja exactamente la manera en la que se soluciona una suma de fracciones con diferente denominador. Ahora bien, podemos ver que la primera fracción (7/3) es una fracción impropia, mientras que (3/4) es una fracción propia. El producto de la operación (37/12) es una fracción impropia.
Ejercicios resueltos de suma de fracciones propias e impropias
Finalmente, vamos a dejarte algunos ejercicios resueltos de suma de fracciones impropias y propias con igual o distinto denominador. Considera los apuntes que hemos dejado para ti y ponlo en práctica.
En este ejercicio, la primera fracción (6/15) es una fracción propia. La segunda fracción (4/15) es una fracción propia. La tercera fracción (20/15) es una fracción impropia.
En este ejercicio, la primera fracción (1/3) es una fracción propia. La segunda fracción (2/4) es una fracción propia.
En este ejercicio, la primera fracción (25/50) es una fracción propia. La segunda fracción (125/50) es una fracción impropia.
En este ejercicio, la primera fracción (2/10) es una fracción propia. La segunda fracción (5/5) es una fracción propia.

