El lenguaje algebraico ha estado ligado a la humanidad desde épocas remotas de la historia antigua, especialmente, en las épocas de grandes civilizaciones como la egipcia y la babilonia. Durante estas épocas, fue un lenguaje algo vago y escueto, sin consistencia ni solidez matemática.
Término algebraico
Con el pasar del tiempo, el lenguaje algebraico fue desarrollando mayor solidez y madurez para comprender y asimilar los problemas de la humanidad. De la mano de los griegos alcanza un punto de inflexión significativo, por medio del enfoque geométrico. Y, finalmente, gracias a los estudios del matemático musulmán Al-Juarismi surgen las bases esenciales de su consistencia conceptual.
Y esto no termina aquí, todavía queda mucho que decir del lenguaje algebraico, por lo que te recomiendo seguir leyendo el artículo.
¿Qué es el lenguaje algebraico?
Después de que Al-Juarismi sentó las bases definitivas del lenguaje algebraico, siguieron años y años de esfuerzo matemático para pulir las imperfecciones y darle mayor extensión y alcance, abarcando aspectos que ni el propio Al-Juarismi alcanzó a vislumbrar.
Con esto dicho, llegamos al año 2019, y el lenguaje algebraico puede ser definido como aquel grupo de símbolos y signos que permiten generalizar relaciones y operaciones puramente numéricas, haciendo posible valorar cualquier condición o combinación de condiciones que se desee, para analizar y comparar situaciones particulares.
El lenguaje algebraico transciende las barreras numéricas del lenguaje aritmético (al cual usualmente se le asocia a la matemática), otorgando una perspectiva más libre y significativa para la matemática, ya que facilita la comprensión de problemas humanos, dándole una matiz pragmática a las matemáticas.
Símbolos y signos del lenguaje algebraico
El lenguaje algebraico, como cualquier otro lenguaje, hace uso de símbolos y signos, los cuales por si mismos no son completamente ajenos a los idiomas conocidos, desde cierta perspectiva. Sin embargo, cuando hablamos de sintaxis y la combinación de estos símbolos y signos ya la mayoría de las similitudes empiezan a desaparecer, debido a la matemática que entra en juego.
La combinación de cada uno de estos símbolos y signos es lo que da el origen de los llamados términos algebraicos, elementos de gran importancia dentro de este lenguaje, siendo el equivalente a las palabras de un idioma.
Por ello, sin más retraso te mencionare estos elementos tan fundamentales para el lenguaje algebraico:
Notación algebraica
La notación algebraica es un concepto que abarca a todo el grupo de símbolos utilizados por el lenguaje. En el lenguaje algebraico se utilizan letras (como cualquier idioma), además de los números, para representar a las cantidades.
Los números son los símbolos que representan a las cantidades conocidas y determinadas. Cuando acompañan a las letras mediante una multiplicación o división son llamados coeficientes; una consecuencia del producto de factores.
Las letras, por su parte, son símbolos que representan a todo tipo de cantidades, es decir, tanto a las conocidas como a las desconocidas. Las primeras letras del alfabeto (a, b, c, d,…) se usan para denotar a las cantidades conocidas, mientras que las últimas letras (z, y, x, w, u,…) representan a las cantidades desconocidas o incógnitas.
Signos de operación
Al igual que en el lenguaje aritmético, en el lenguaje algebraico también se llevan a cabo operaciones como la suma, la resta, la multiplicación, la división, por lo que se usan los signos +, -, * y /, respectivamente.
No hay que olvidar la potenciación y la extracción de raíces. Para estas operaciones, el lenguaje algebraico sigue siendo igual al aritmético, adoptando la relación base/ exponente para la potenciación (
) y el signo radical 
para la extracción de raíces.
Signos de relación
Estos signos permiten relacionar entre sí tanto a los símbolos como a las operaciones aritméticas anteriormente nombradas. En el lenguaje algebraico, principalmente se utilizan los siguientes signos:
- El signo = representa una igualdad. De esta forma, la relación
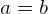quiere decir que a es igual a b - El signo < representa una desigualdad, en la cual el símbolo de la izquierda es menor que el de la derecha. Con esto tenemos que la relación
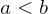significa que a es menor que b - El signo > se encarga de representar una desigualdad en la que el símbolo de la izquierda, ahora, es mayor que el de la derecha. Es decir, la relación
indica que a es mayor que b
Signos de agrupación
Estos signos son el conocido paréntesis ordinario (), el corchete [] (o paréntesis angular) y las llaves {}. Estos son los principales, pero adicionalmente existe la barra o vínculo ‾‾‾‾.
Todos estos signos funcionan para jerarquizar la prioridad y orden de las operaciones. Toda operación que se encuentre contenida dentro de ellos debe realizarse primero que cualquier otra, según determinadas reglas. Por ejemplo, las siguientes operaciones de términos algebraicos 
, por el paréntesis la suma entre a y b debe ser realizada primeramente, antes del producto con d.
Compresión del lenguaje algebraico
Ahora que hemos conocidos a los símbolos y signos del lenguaje algebraico, es hora de aprender a formar palabras y oraciones, o su equivalente, para ser más precisos.
El término algebraico es el equivalente a una palabra, en este lenguaje matemático. Este término es una expresión algebraica la cual puede estar formada por un solo símbolo o por varios, no separados entre sí por los signos de operación. En términos concretos, está compuesto por un signo, un coeficiente, una parte literal y un grado.
De seguro debes de preguntarte entonces: ¿Qué es una expresión algebraica? Ciertamente, puede parecer que esta debe de ser la forma más simple del lenguaje algebraico, pero esto no es del todo cierto. Una expresión algebraica es definida como la representación de un símbolo o de una o varias operaciones entre símbolos. Por ello, es tanto lo más simple como lo más complejo; una interesante generalización conceptual.
En realidad, el equivalente exacto de una palabra en el lenguaje algebraico es el monomio y el correspondiente equivalente a una oración es el polinomio. Así, tenemos que el monomio es la expresión algebraica más simple, mientras que el polinomio es la más compleja.
Uno de los monomios más conocidos son los que determinan del área de figuras geométricas sencillas (planas) como los cuadrados, rectángulos y rectángulos. Para el área un cuadrado con a unidades de lado, tenemos la siguiente expresión: 
que forma parte de la fórmula para el área 
. Recordando un poco de geometría elemental, podemos obtener las siguientes formulas adicionales:
La primera fórmula representa el área de un rectángulo de lados a y b unidades, y la segunda, representa el área de un triángulo de base b y una altura h. Con estas fórmulas generalizadas es posible obtener el área de cualquier cuadrado, rectángulo y triángulo que puedas imaginar, te invitamos a probar estas fórmulas.
