Si quieres aprender cómo resolver problemas de suma de fracciones distinto denominador, has llegado al lugar indicado. En este material vamos a repasar en qué consiste este tipo de operaciones matemáticas, en qué caso se aplican y los métodos que existen para efectuar la suma de fracciones.

Del mismo modo, podrás aprender de forma práctica cómo resolver operaciones con fracciones cuando hay distintos denominadores en las partes involucradas, para ello dejamos para ti una serie de ejemplos, ejercicios resueltos y para resolver. Y como no puede faltar, algunas aplicaciones a la vida cotidiana de la suma de fracciones con distinto denominador.
Continúa leyendo para aprender todo lo que necesitas sobre una de las operaciones matemáticas más útiles de todas, desde su implementación en civilizaciones antiguas como la egipcia y la babilónica.
Cómo hacer suma de fracciones con distinto denominador
Para resolver suma de fracciones con diferente denominador, en esencia, se busca homogenizar los denominadores de cada uno de los elementos que forman parte de la suma. De esta manera resulta más sencillo efectuar la suma de fracciones. Para ello, se aplican dos métodos bastante simples y efectivos.
A continuación se explica como resolver suma de fracciones distinto denominador utilizando el método de la cruz y el método del mínimo común múltiplo (m.c.m). Presta atención y toma nota.
Suma de fracciones con diferente denominador por método de la cruz
El método de la suma de fracciones diferente denominador mediante el método de la cruz, también llamado multiplicación en cruz es a priori, la manera más sencilla de resolver este tipo de operaciones. A continuación explicamos este método con un ejemplo:
![]()
Esta operación está compuesta por dos fracciones, la primera de ellas es 1/3 y la segunda ½. Como se puede apreciar, se trata de una operación de distintos denominadores, siendo (3) el denominador de la primera fracción y (2) el denominador de la segunda.
Efectuar la operación de suma de fracciones con distinto denominador en este caso, consiste en realizar un artificio matemático que permita convertir ambos denominadores en uno igual. Para ello, se multiplican ambos denominadores (3×2=6), y el resultado (6) se sustituye en la operación como nuevo denominador común.
![]()
Ahora es necesario conseguir los numeradores equivalentes para la operación de manera tal que se conserven las proporciones reales de la fracción. Para ello, se debe realizar una multiplicación en forma de cruz, es decir, el numerador de la primera fracción (1) por el denominador original de la segunda (2), de esta forma se obtiene el nuevo numerador de la primera fracción (1×2=2)
Lo mismo se aplica para el nuevo segundo numerador, (1×3=3). De esta forma obtenemos lo siguiente:
![]()
En esta instancia, como es evidente, nos encontramos frente a una suma de fracciones con el mismo denominador. Por lo que la operación la podemos resolver aplicando la adición a los numeradores y manteniendo el denominador común.
![]()
Ejemplos de suma de fracciones con distinto denominador con el método de la cruz
Para reforzar este contenido, a continuación dejamos para ti suma de fracciones con diferente denominador ejemplos resueltos.
Suma de fracciones con diferente denominador por método de m.c.m
El segundo método empleado para realizar la suma de fracciones distinto denominador mediante el uso del mínimo común múltiplo con la intención de obtener un nuevo denominador común para la operación y así poder dar con el resultado.
El primer ejemplo que veremos será el siguiente:
![]()
En este caso, se trata de una suma de fracciones heterogéneas, dado que las dos fracciones involucradas poseen un denominador diferente, en este caso (6) y (3) respectivamente para la primera y segunda fracción.
Para esta operación empezaremos por obtener el mínimo común múltiplo de ambos denominadores.
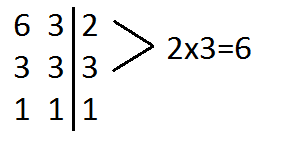
En este caso se han descompuesto los dos valores en números primos hasta dar con el mínimo común múltiplo de (3) y (6). El nuevo valor obtenido (6) será el nuevo denominador común de nuestra suma de fracciones.
![]()
En este caso, es necesario que los numeradores sigan manteniendo la proporcionalidad con respecto al nuevo denominador. En la primera fracción (5/6), como el denominador es el mismo, no es necesario realizar ningún cambio en el numerador. Sin embargo, para la segunda fracción (2/3) es necesario aplicar un artificio matemático que permita obtener la nueva fracción.
Para resolver esto, es necesario multiplicar tanto el numerador, como el denominador por un mismo número que garantice la homogeneidad de la operación. Dicho de otra forma, debemos multiplicar el denominador de fracción por un número que de como resultado (6), pero al hacer esto, se debe multiplicar el mismo número por el numerador. Lo ejemplificamos de forma sencilla:
![]()
En este caso podemos simplificar la operación y obtendríamos:
![]()
Es evidente que ahora nos encontramos frente a una suma de fracciones homogéneas (igual denominador), por lo que podemos dar resolución a la operación sumando los numeradores y manteniendo el denominador común.
![]()
Este proceso también puede ser aplicado a la suma o resta de dos o más fracciones, lo importante es aplicar el método de mínimo común múltiplo a todos los denominadores distintos de la operación.
Aplicaciones y ejercicios propuestos de suma de fracciones con distinto denominador
Para reforzar el aprendizaje dela suma de fracciones distinto denominador resulta esencial la práctica y el análisis. Por eso, dejamos para ti algunos casos de aplicaciones de la suma de fracciones para ver cómo se aplican estas operaciones a problemas de la vida cotidiana.
Del mismo modo, si quieres practicar tú mismo problemas de suma de fracciones con distinto denominador, dejamos algunos ejercicios propuestos.
Aplicaciones de suma de fracciones ejercicios resueltos
Caso 1
Un lector empedernido logra leer ¼ parte de su biblioteca durante los primeros 3 meses del año. Luego, el segundo trimestre lee 1/5 parte de toda su estantería de libros. Después, en época de vacaciones termina de leer 1/3 parte de todos sus libros.
- Para finales de sus vacaciones, ¿qué parte de su librería ha logrado leer esta persona?
![]()
Para finales de vacaciones, este lector ha leído un total de 47/60 partes de su librería, lo equivalente a 78% de su librería.
Caso 2
Una empresa vendedora de trigo logra vender durante su primer año 2/8 toneladas de material. Después, al segundo año de ventas logra incrementar sus ventas al vender 2/5 toneladas de trigo. Al tercer año se logran alcanzar mejores ventas, logrando vender ½ toneladas de este producto.
- A finales del tercer año ¿Cuántas toneladas de trigo ha logrado vender?
![]()
A finales del tercer año esta empresa ha logrado vender 92/80 toneladas de trigo, es decir 1,15 toneladas.
Caso 3
Un programador se encarga de subir grandes cantidades de datos a la nube. En una semana logra cargar a la nube 3/10 partes de todos los archivos que necesitan cargarse. Durante la segunda semana puede subir 2/9 partes de los datos. Finalmente a la tercera semana es capaz de subir 1/7 partes de todo el contenido.
- Aplicando la suma de fracciones distinto denominador, ¿Cuántas partes de todos los datos digitales ha logrado subir este programador a la nube?
![]()
Ejercicios de suma de fracciones distinto denominador para resolver
Si quieres practicar la suma de fracciones con distinto denominador con cualquiera de los métodos posibles, a continuación facilitamos algunos ejercicios para practicar.
