El valor numérico de una expresión algebraica es la mejor forma de romper las abstracciones, que tanto abundan en el álgebra. Es que, ciertamente, el álgebra se encuentra repleta de abstracciones y aspectos imaginativos, cuestiones puramente matemáticas a las cuales puede resultar difícil hallar la utilidad práctica.
Sin embargo, las matemáticas, y consecuentemente, el álgebra, han demostrado ser plenamente valiosas y útiles para la humanidad desde épocas antiguas; ayudando a erigir maravillosas civilizaciones como la egipcia, la babilonia y la asiria, por mencionar algunas. Por mucho que puedas ver a las abstracciones como los pasatiempos de los matemáticos modernos y eruditos antiguos, no hay que subestimar esta herramienta sorprendente del pensamiento humano.
El álgebra está en una de las ramas más fundamentales de la matemática, por ello, las generalizaciones que se obtienen mediante sus abstracciones, permiten transcender las limitaciones numéricas de la aritmética, dando origen a expresiones libres y versátiles, capaces de adaptarse a la voluntad. Esto y muchas cosas más entran dentro de las implicaciones del valor numérico de una expresión algebraica, así que, lector, te invito a continuar leyendo.
¿Qué es el valor numérico de una expresión algebraica?
Al valor numérico de una expresión algebraica se le conoce como la consecuencia de sustituir a las letras de un término algebraico dado por cualquier número que se quiera (dentro de ciertos límites), realizando luego las operaciones correspondientes.
Como ya te mencionamos previamente, si quieres dejar a un lado las abstracciones del álgebra, representadas por las letras, aplícale a la parte literal de un término algebraico un valor numérico, es decir, asígnale algún número, para acabar con la generalización y obtener resultados particulares.
Desde el comienzo hasta el final de la travesía por el país del álgebra, en cualquiera de sus rincones, se puede ver que hay una predominancia desconcertante de letras sobre los propios números; las bases de la matemática. Esta cuestión no implica una desvinculación aberrante por parte del álgebra, sino más bien, una nueva perspectiva, más avanzada que la ofrecida por la aritmética, en la que cada letra, realmente, representa (casi) cualquier número concebible.
En efecto, esas letras que puedes ver en un término algebraico, inherentemente, representan a todos los números (preferiblemente a los racionales positivos, junto con el cero). Así que, en realidad, no existe ninguna predominancia, todo es una ilusión provocada por la generalización del álgebra.
El valor numérico de una expresión algebraica es la prueba irrefutable del poder matemático de las generalizaciones, puesto que ayudan a encapsular elementos extensos en una única expresión, que puede adaptarse relativamente a cualquier condición.
¿Cómo hallar el valor numérico de expresiones algebraicas?
Hallar el valor numérico de una expresión algebraica forma parte del grupo de tareas más simples en el álgebra, porque todo se reduce a sustituir las letras por los números dados y, resolver las, ahora desbloqueadas, operaciones aritméticas, ya sea una multiplicación, división, potenciación, suma o resta.
Pero, hay que resaltar que debido a que existen diferentes términos algebraicos, como son los monomios, binomios y polinomios (englobando a todos los demás), hay que proceder concienzudamente para obtener el valor numérico verdadero de las expresiones.
Debido a la diversa configuración de las expresiones algebraicas, te presentamos a continuación, los 2 casos para resolver y obtener el valor numérico de cualquier expresión con la que puedas encontrarte.
Valor numérico de expresiones simples
Para comenzar a calentar motores, empecemos con la expresión algebraica más sencilla, es decir, los monomios. Observa y analiza la resolución de los siguientes ejemplos de términos algebraicos:
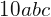 para a=2, b=3, c=5
para a=2, b=3, c=5
Como puedes ver, se necesita de una serie de condiciones iniciales para poder obtener el valor numérico de una expresión algebraica. Esto será una constante, tanto para el caso de los monomios, como el de los binomios y polinomios.
Ahora, lo que queda por hacer es sustituir a cada letra por su respectivo número, desarrollando las operaciones expresadas por el monomio. Por lo que, tendremos lo siguiente:
![]()
Probemos con otros ejemplos, más complejo.
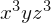 para x=2, y=7, z=4
para x=2, y=7, z=4
Sustituyendo y resolviendo, tenemos:
![]()
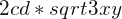 para x=3, y=9, c=1/2, d=1/3
para x=3, y=9, c=1/2, d=1/3
![]()
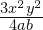 para x=1/4, y=2, a=3, b=1/2
para x=1/4, y=2, a=3, b=1/2
![]()
Valor numérico de expresiones compuestas
Abarcado el caso más sencillo de resolución, es turno de adentrarnos en lo más interesante del valor numérico de expresiones algebraicas, de los binomios y polinomios, por supuesto.
Adentrarnos en esta sección es el paso para comprender la solución de ecuaciones, obteniendo el valor de determinadas incógnitas, pero, esto no termina allí, ya será cuestión de profundizar más de este tema tan importante del álgebra, pero en otro artículo.
Regresando a lo que nos interesa a priori, con los siguientes ejemplos de términos algebraicos podrás ver que hallar el valor numérico de binomios y polinomios es tan sencillo como el caso de los monomios; todo se centra en sustituir y operar. La única diferencia radica en el hecho de que deberán hacerse operaciones aritméticas adicionales. Sin más vueltas al asunto, aquí están los ejemplos:
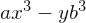 para a=12, x=3/2, y=34, b=1/2
para a=12, x=3/2, y=34, b=1/2
![]()
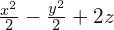 para x=3, y=4, z=6
para x=3, y=4, z=6
![]() para x=2, a=1/2, y=3, b=2/3, z=3/4
para x=2, a=1/2, y=3, b=2/3, z=3/4
![]()
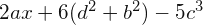 para a=1/4, x=2, b=3, d=4, c=7/2
para a=1/4, x=2, b=3, d=4, c=7/2
![]()
Ejercicios propuestos para hallar el valor numérico de expresiones algebraicas
Cómo pudiste ver con los ejemplos anteriores, hallar el valor numérico no requiere de tanto cálculo y análisis, ya que involucra operaciones aritméticas, las cuales son ampliamente conocidas. Esto es básicamente como introducir valores en formulas, ya sea para obtener el volumen, el área o la densidad de algún objetivo. De allí estriba la sencillez matemática de este tópico.
Ahora que han sido finalizados los ejemplos para hallar los valores numéricos de expresiones algebraicas, con el objeto de progresar en la compresión de las generalizaciones más esenciales del álgebra, a continuación te dejaremos algunas expresiones algebraicas a las cuales debes buscar su valor numérico según las condiciones que se indiquen.
Halla el valor numérico de las siguientes expresiones para los valores:
a=3, b=2, c=1/3, d=4, m=6, n=1/4
